主成分分析（PrincipalComponentAnalysis，简称PCA）是一种常用的多变量数据降维方法，通过线性变换将原始数据映射到新的坐标系中，使得数据在新坐标系下具有最大的方差。本文将详细介绍主成分分析的原理、计算方法、结果解读以及实际应用场景。

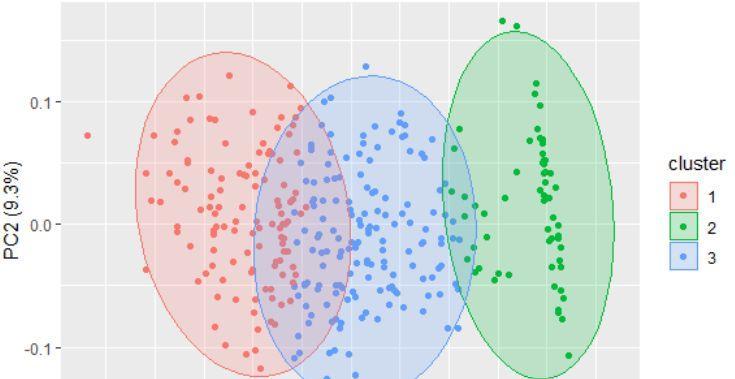
1.主成分分析的基本原理

主成分分析的核心思想是将高维度数据转化为低维度数据，保留大部分原始数据的信息。通过数学方法，PCA找到一组正交基，使得数据在新坐标系下的方差最大。这些正交基被称为主成分，可以理解为新坐标系的轴向量。

2.主成分分析的计算方法

主成分分析的计算可以通过协方差矩阵的特征值分解来实现。计算原始数据的协方差矩阵；对协方差矩阵进行特征值分解，得到特征值和特征向量；选择最大的k个特征值对应的特征向量作为主成分。

3.解读主成分分析的结果

主成分分析的结果包括主成分的方差解释率、主成分系数和主成分载荷。方差解释率表示每个主成分对总方差的贡献程度；主成分系数表示原始变量与主成分之间的线性关系；主成分载荷表示原始变量在每个主成分中的权重。

4.主成分分析的应用场景

主成分分析在各个领域都有广泛的应用，例如数据降维、图像处理、模式识别等。在数据降维中，主成分分析可以帮助提取重要特征，减少特征维度，提高数据处理效率。在图像处理中，主成分分析可以用于图像压缩和图像恢复。在模式识别中，主成分分析可以用于特征提取和分类。

5.主成分分析与其他降维方法的比较

与其他降维方法相比，主成分分析具有简单易懂、计算高效和无监督学习等优点。与线性判别分析相比，主成分分析不考虑样本类别信息，因此适用于无监督学习场景。

6.主成分分析的局限性及应对策略

主成分分析也存在一些局限性，比如对异常值敏感、无法处理非线性关系等。为了克服这些问题，可以采用数据预处理、核主成分分析等方法来改进主成分分析的性能。

7.主成分分析在金融领域的应用

在金融领域，主成分分析可以用于股票投资组合优化、风险管理和信用评级等方面。通过对股票数据进行主成分分析，可以构建具有较小方差的有效投资组合，降低投资风险。

8.主成分分析在医学领域的应用

在医学领域，主成分分析可以用于研究疾病相关因素、诊断和预测等。通过对医学数据进行主成分分析，可以找到与疾病相关的主要特征，辅助医生进行诊断和治疗。

9.主成分分析在社会科学领域的应用

在社会科学领域，主成分分析可以用于研究人群特征、心理评估和调查问卷等。通过对社会科学数据进行主成分分析，可以提取出代表性的主成分，揭示人群特征和行为规律。

10.主成分分析在工业领域的应用

在工业领域，主成分分析可以用于质量控制、故障诊断和产品设计等方面。通过对工业数据进行主成分分析，可以提取出与产品质量相关的主要特征，改进产品设计和生产流程。

11.主成分分析在市场研究领域的应用

在市场研究领域，主成分分析可以用于消费者行为分析、市场细分和品牌定位等。通过对市场数据进行主成分分析，可以发现潜在的市场细分群体，指导企业制定营销策略。

12.主成分分析在大数据分析领域的应用

在大数据分析领域，主成分分析可以用于数据可视化、模式发现和异常检测等方面。通过对大数据进行主成分分析，可以发现隐藏在海量数据中的规律和异常，为决策提供支持。

13.主成分分析在生态环境领域的应用

在生态环境领域，主成分分析可以用于环境监测、生态评估和资源利用等。通过对环境数据进行主成分分析，可以揭示不同因素对生态系统的影响，为环境保护和资源管理提供参考。

14.主成分分析在教育评价领域的应用

在教育评价领域，主成分分析可以用于学生综合素质评价和教育质量评估等方面。通过对学生成绩和学生行为数据进行主成分分析，可以综合评价学生的综合能力，指导教育改革和发展。

15.

主成分分析是一种常用的多变量数据降维方法，能够提取重要特征、减少特征维度，并广泛应用于各个领域。通过本文的介绍，读者对主成分分析的原理、计算方法、结果解读以及实际应用场景有了更深入的理解，希望能够对读者在实际工作和研究中有所帮助。